Example Multiple Choice Questions
Psychology 2300 - Introduction to Statistics
Instructor - Dr Jeremy Jackson
Week 1
1) If X = {1, 2, 3} then ΣX is:
a) 3
b) 6
c) 1
d) None of the above
2) The sigma sign (Σ) means:
a) Sum all the values of X
b) Sum all the values
c) Sum all the values to the right of the sign
d) Sum all the values to the left of the sign
e) Sum all the values in the population
3) Another way to say "ΣX" is:
a) The total of all the values
b) The sum of the values
c) Add up all the values
d) All of the above
e) None of the above
4) Xi means:
a) All the values of X
b) The first value of X
c) X
d) The ith value of X
e) None of the above
5) If X= {3, 5, 7}, and i=2, Xi is:
a) 5
b) 3
c) 8
d) 7
e) None of the above
6) It was argued in class that the real problem of understanding introductory statistics is NOT ________ but ________.
a) mathematical, linguistic
b) intelligence, mathematical ability
c) algebra, mathematical ability
d) effort, talent
e) None of the above
7) It was argued in class that some students will not be successful in this class because they __________ at ___________.:
a) are not sufficiently talented, math
b) do not learn the meaning of statistical concepts, the time they are introduced in the course
c) become anxious, the time of the test
d) have no interest in statistics, this time in their lives
e) None of the above
8) It was argued in class that the two big differences between statistics courses and many of the courses with which students may well be familiar is that statistics courses are __________ and _________:
a) fascinating, inspirational to students
b) irrelevant, disliked by students
c) hard, boring
d) cumulative, require precise definitions of terminology
e) None of the above
9) The question of how to be successful in this course was discussed at length in class. The instructor recommended that students do 4 things to ensure their success. They were:
a) study hard, be proactive, read the text carefully, get a tutor
b) highlight important sections of the text, find a way to get excited about statistics, cram, have fun in class
c) form a study group, work harder as the course progresses, don't worry about definitions, don't memorize...understand
d) make cue cards with the name and symbol for the concept on one side and the definition and an example on the other, make cue cards for concepts immediately when they are introduced and carry them with you at all times, use downtime (like waiting for the bus) to learn the cue cards...not text friends, at the end of every class review your notes, write down any questions you have and ask them at the beginning of the next class.
10) If x={1, 2, 3, 4, 5}, Σ(x-x̄) is:
a) 15
b) 5
c) unknown
d) never 0
e) always 0
11) Another way to say "xi-x̄ " is:
a) The sum of the deviation scores
b) A deviation score
c) 0
d) The distance and direction a score is from the mean of the distribution
e) b & d
12) In words the following "Σ(x-x̄)" means:
a) The total distance all scores are from the mean
b) Subtract each value of x from the mean
c) Add up the values of x and subtract the result from the mean
d) Take each value of X, subtract the mean from it, do this for all values of X and then add up the resulting values
e) The sum of squares
13) In words the following "Σ|x-x̄|" means:
a) The total distance scores are from the mean
b) The AAD
c) The average distance scores are from the mean
d) The distance a score is from the mean
e) The sum of the deviation scores
14) In class, it was argued that we make students take this course because:
a) Students need to know how to read academic papers with statistical methods in them
b) Statistics is really important
c) All nurses need to understand basic statistical theory
d) The more students that take statistics courses, the more jobs there are for teachers of statistics
e) The purpose of an undergraduate education is to teach students to write, speak and think in multiple domains of inquiry. Statistics/math is one of those domains of inquiry (as are history, science, literature, etc).
Week 2
1) Inferential statistics is:
a) The practice of summarizing a set of raw data
b) The theory and methods relevant to the estimation of central tendency
c) The theory and methods of using sample information to test hypotheses about population parameters
d) The theory and methods of using population information to test hypotheses about sample statistics
2) The three key issues of descriptives statistics as discussed in class are:
a) Reliability, validity, sensitivity
b) Accuracy, precision, validity
c) Summarization, representation, loss
d) Random sampling, null hypothesis, critical value
e) Shape, location, spread
3) The sum of the deviation score is:
a) 0
b) Never 0
c) Depends on the data
d) Larger than the mean
e) None of the above
4) The difference between the population parameter and sample statistic is called:
a) Sampling error
b) Random error
c) Measurement error
d) Deviation score
e) None of the above
5) The mean of the values in your population bag is:
a) A parameter
b) A statistic
c) Close to 3
d) A variable
e) None of the above
6) We are interested in the effect of the _____ on the _______:
a) Parameter, Statistic
b) IV, DV
c) DV, IV
d) Statistic, Parameter
e) None of the above
7) Male is a __________ of a __________:
a) variable, level of a variable
b) level, variable
c) variable, gender variable
d) Statistic, Parameter
e) None of the above
8) Gender is a __________ variable:
a) Dichotomous
b) Continuous
c) Discrete
d) Ordinal
e) The number of levels depends upon how gender is defined
9) If we are interested in the effect of gender on happiness, gender is a _____ and happiness is a _____:
a) DV, IV
b) Parameter, statistic
c) IV, DV
d) IV, IV
e) Level of an IV, DV
10) If we are interested in the effect of gender on happiness, gender is a _____ and happiness is a _____:
a) DV, IV
b) Parameter, statistic
c) IV, DV
d) IV, IV
e) Level of an IV, DV
11) The shape of the distribution of values in your population bag is:
a) Unimodal
b) Skewed
c) Uniform
d) Normal
e) Polychotomous
12) The shape of the distribution of time to recommitting a crime after release from jail is:
a) Unimodal
b) Skewed right
c) Skewed left
d) Normal
e) Polychotomous
13) The shape of a distribution of exam scores for a class made-up of two groups of students, one group that studies a lot and another group that does not study at all will be:
a) Unimodal
b) Skewed right
c) Bimodal
d) Normal
e) Polychotomous
14) In a distribution that is heavily skewed to the left, most of the scores are _______ of the distribution:
a) On the left side
b) On the right side
c) In the center
d) On the left side and right side but not in the center
e) Can not tell where most of the scores would be
15) If a distribution is _________ it can not be _____________:
a) Skewed, unimodal
b) Skewed left, skewed negatively
c) Bimodal, symmetrical
d) Skewed right symmetrical
e) None of the above
16) The largest deviation score in your population bag is associted with the raw score of:
a) 3
b) 2
c) 5
d) 1
e) Can not be determined
17) The sum of the absolute deviation scores in your popluation bag is:
a) 0
b) 9
c) 5
d) 6
e) 36
18) The sum of the squared deviation scores in your popluation bag is:
a) 0
b) 6x6
c) 50
d) 60
e) 36x36
19) The sum of the squared deviation scores is 0 when:
a) All the deviation scores are the same
b) The mean is 0
c) The sum of the deviation scores is 0
d) All the scores in the distribution are the same
e) None of the above
20) An absolute deviation score is:
a) Always 0
b)The distance a score is from the mean of the distribution of scores
c) The distance and direction a score is from the mean of the distribution of scores
d)The sum of the distances scores are from the mean
e) None of the above
Week 3
1) The _______ is the sum of the scores divided by the total number of scores:
a) Mode
b) Mean
c) Median
d) Sum
2) In the following set of scores the ________ is larger than the _______: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5
a) Mean, mode
b) Mean, median
c) Median, mean
d) The mean, median and mode are all the same
e) None of the above
3) If we added 2 values of "5" to the following set of scores, the mean would _____ and the median would _____: 1, 1, 2, 2, 3, 3, 4, 4, 5, 5
a) Get larger, get smaller
b) Get smaller, get larger
c) Get larger, get larger
d) Get smaller, get smaller
e) Get larger, stay the same
4) The appropriate measure of location for most survival data is:
a) Mean
b) Median
c) Mode
d) All three are as good as each other
5) The average distance scores are from the mean of a distribution is known as:
a) The variance
b) The mean
c) The AAD
d) Sum of squares
e) Sum of the deviation scores
6) The deviation score for a value of 1 in a distribution with a mean of 3 is:
a) -1
b) 1
c) 2
d) -2
e) Can not tell
7) The number of deviation scores in a distribution of scores is:
a) 1
b) The same as the number of raw scores
c) The number of raw scores minus 1
d) 2
e) None of the above
8) The sum of the deviation scores is:
a)1
b) 0
c) The sum of squares
d) The AAD
e) None of the above
9) The distance the score of -1 is from the score of 4 is:
a) -4
b) 5
c) -5
d) 4
e) None of the above
10) The AAD of 10,000 0's and 10,000 -1's is:
a) 0
b) 1
c) 1/2
d) -1
e)1/4
11) The AAD of 1, 1, 2, 2, 3, 3, 4, 4, 5, 5 is:
a) 1.2
b) 2
c) 1.414
d) 12
e) None of the above
12) In a distribution that is skewed to the right, the mean is:
a) Larger than the mode
b) The same as the median
c) Smaller than the median
d) Smaller than the mode
e) None of the above
13) If a value of 3 is added to a distribution of scores with mean of 3, this will:
a) Increase the variance
b) Not influence the variance
c) Increase the mean
d) Decrease the mean
e) None of the above
14) If we add a value of 3 to a distribution with 10,000 2's and 10,000 4's this will:
a) Decrease the mean
b) Decrease the AAD
c) Increase the AAD
d) Increase the mean
e) Can not tell what will happen to the mean or AAD
15) If the variance is 1:
a) The mean is also 1
b) The mean is 0
c) The SD is 1
d) The SD is less than 1
e) None of the above
Week 5
1) The mean and standard deviation of a set of standard scores is:
a) 1, 0
b) 1, 1
c) 0,0
d) 0, 1
2) The standard score associated with the raw score value of 5 in the following set of scores is: 5, 5, 7, 7
a) 5
b) 0
c) -1
d) 1
e) None of the above
3) If the mean on the first quiz in the class is 70% and the SD is 10%, what score did you get if your standard score is 2.5?
a) 90%
b) 55%
c) 85%
d) 70%
e) None of the above
4) If the standard deviation of a set of scores is 10, what would the standard deviation be if we divided every score in the distribution by 10:
a) 10
b) 0
c) 1/10
d) 1
e) Not enough information
5) The shape of a distribution of standard scores is:
a) The same as the shape of the distribution of raw sores
b) Normal
c) Close to Normal
d) Not enough information to tell
e) None of the above
6) If X is discrete, the pairing of the values of X with their associated probabilities is a:
a) Probability distribution
b) Probability density function
c) Uniform distribution
d) Normal distribution
e) Frequency distribution
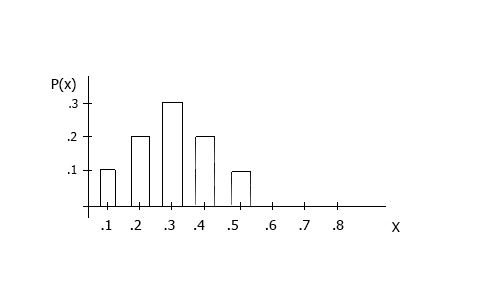
7) The distribution below is a:
a) Probability distribution
b) Probability density function
c) Frequency distribution
d) population distribution
e) None of the above
8) In the distribution below the P(X>.4) is:
a) 0
b) .4
c) .2
d) 1
e) None of the above
9) In the distribution below the P(X=.3 or X=.4) is:
a) .5
b) .3
c) 1
d) .2
e) None of the above
10) The Normal distribution is:
a) A probability density function
b) Theoretical
c) A good model for the distribution of IQ scores
d) Never found in reality
e) All of the above
11) The distribution of IQ scores is:
a) Normal
b) Theoretical
c) A probability density function
d) All of the above
e) None of the above
12) In a uniform distribution (assume it is a PDF) in which 1 < X < 5, the P( X > 1) is:
a) 1
b) .25
c) 0
d) .75
e) None of the above
13) In the distribution given in question 12, what is P(X >2):
a) 0
b) .5
c) .25
d) 1
e) None of the above
14) In the distribution given in question 12, what is P(X=2):
a) .25
b) .75
c) 0
d) very small
e) None of the above
15) The variance of the standard Normal distribution is:
a) The same as the variance of the raw scores
b) 1
c) 0
d) Unknown
e) Sigma squared
Week 6
1) The area above one standard deviation above the mean in a Normal distribution is:
a) .16
b) .14
c) .34
d) .84
2) If X is uniform and continuous and 1 < X < 11, the probability that X is between 3 and 4 is:
a) 1
b) .2
c) .1
d) Can not be determined
e) Close to .1
3) If the mean of the distribution of IQ scores is 100 and the SD is 15, what is the probability that a randomly sampled individual will have an IQ score greater than 130?
a) .02
b) .14
c) .001
d) .5
e) Can not be determined
4) The Normal Distribution is:
a) A good model for the distribution of IQ scores
b) An empirical distribution
c) A poor model for the distribution of IQ scores
d) The same shape as the distribution of IQ scores
5) If a tomato producer knows that the mean volume of their tomatoes is 5 cubic cm and the SD is 2 cubic cm, what is the probability that a tomato will be less than 3 cubic cm (assume the distribution of tomato volumes is modeled well by a Normal distribution):
a) Approximately .14
b) Approximately .16
c) Exactly .16
d) Exactly .14
e) Unknown
6) From question 5, if the tomato producer knows that customers will never select a tomato if it is less than 1 cubic cm (they will let it rot in the store), out of 1,000 tomatoes delivered to the store, how many will go unsold:
a) 100
b) 200
c) 210
d) 20
e) 2
7) From question 5, one week, the owner of a grocery store notices that they seem to be getting a very large number of small tomatoes from the tomato producer. They decide to count the number of tomatoes they received in their latest shipment that are less than 1 cubic cm in size. They find that 10% of the tomatoes they revived were less than 1 cubic cm in size. They should:
a) Not worry too much because this is about how many tomatoes one would expect to be less than 1 cubic cm
b) Inform the producer that the percent of tomatoes below 1 cubic cm is much greater than it should be
c) Get out of the grocery business and go to Hawaii
8) The Normal distribution and t-distribution are:
a) The same shape
b) Similar in shape
c) Similar in shape if the degrees of freedom is high
d) Similar in shape if the degrees of freedom is low
e) None of the above
9) The t-distribution has:
a) Fatter tails than the Normal distribution
b) Thiner tails than the Normal distribution
c) No tails
d) A platykurtic shape
e) None of the above
10) The t-distribution:
a) Is a PDF
b) Has an area of 1
c) Has f(x) > 0 for all values of t
d) a and b but not c
e) a, b and c
11) A likert scale is:
a) Dichotomous
b) Nominal
c) Continuous
d) Polychotomous
e) None of the above
12) If X~N, p( X > 10) is .16 and the mean of X is 5, the SD of X is:
a) 1
b) 5
c) 10
d) 15
e) None of the above
13) In question 12, the Z-score associated with the value of 0 is:
a) .34
b) 1
c) 10
d) -1
e) None of the above
14) If mu is -5 and sigma is 5, P(x>5) is:
a) 1
b) .5
c) 0
d) Undefined
e) None of the above
15) If X~Standard Normal, p(X>-1) is:
a) .16
b) -.16
c) .84
d) .34
e) None of the above
Week 7
1) The population from which a sample is drawn is:
a) Always Normal in shape
b) Bigger in size than the sample size (N is greater than n)
c) A large number of subjects or people
d) None of the above
2) The probability of 2 heads when we flip a coin twice is:
a) 1
b) .5
c) .25
d) .75
e) Unknown
3) How many possible values of the variable "# of heads when a coin is flipped 4 times" are there:
a) 5
b) 4
c) 1
d) .25
e) Can not be determined
4) Assume a coin is equally weighted on both sides, what is the probability of 0 or 1 heads when it is flipped 3 times:
a) 1/8
b) 3/8
c) .5
d) Can not be determined
5) if we are interested in the sampling distribution of the number of heads when a fair coin is flipped 3 times, what is the sample size:
a) 8
b) 3
c) 2
d) .5
e) Unknown
6) Imagine we sample 2 values from your population bag, what is the probability that the lowest number in the sample is 1:
a) 5/25
b) 9/25
c) 7/25
d) 1/25
e) None of the above
7) As the sample size increases:
a) The SD of the sample goes down
b) The SD of the sample stays the same
c) Sampling error goes down
d) Sampling error goes up
8) The shape of the sampling distribution of the mean is:
a) The same as the shape of the population
b) The same as the shape of the sample
c) Approximately Normal
d) Exactly Normal
e) None of the above
9) The mean of the sampling distribution of the mean is:
a) The same as the mean of the population
b) The same as the mean of the sample
c) Approximately the same as the mean of the population
d) Approximately the same as the mean of the sample
e) None of the above
10) The distribution of the sample SD calculated on all possible samples of a given size drawn from a well defined population is:
a) The sampling distribution of the mean
b) The sampling distribution of the SD
c) The sample distribution of the SD
d) There is no such thing
11) If the standard error of the mean is 10 and the sample size is 16, what is the standard deviation of the population:
a) 10
b) 40
c) 10/16
d) 160
e) None of the above
12) If the mean of the population is 10, the SD of the population is 10 and the population is close to Normal in shape, what is the probability of getting a sample mean greater than 10 when the sample size is 25:
a) .16
b) .34
c) .84
d) .5
e) None of the above
13) In question 12, what would happen to the probability of getting a sample mean greater than 10 if the sample size increased:
a) It would stay the same
b) It would go up
c) It would go down
14) Consider question 12, would we get a sample mean of 16 or more very often if we were to sample 25 values from this population:
a) Yes
b) No
c) Unknown
15) If we were to flip a coin 5 times, would we get 5 heads very often:
a) Yes
b) No
c) Unknown
Week 9
1) The null hypothesis is the hypothesis:
a) That we would like to reject
b) Of no difference
c) Of no difference between treatment means
d) That the IV has no effect on the DV
2) The probability the null hypothesis is true is:
a) The p-value
b) One minus the p-value
c) Usually high
d) Usually low
e) There is no such thing
3) In a court of law the principle that the accused is presumed innocent prior to the evaluation of the evidence is logically equivalent to:
a) The null hypothesis
b) The p-value
c) The attendant assumptions
d) The critical value
e) None of the above
4) In hypothesis testing, the decision rule is:
a) Accept the null if the p-value is high
b) Accept the null if the p-value is low
c) Reject the null if the p-value is high
d) Reject the null if the p-value is low
5) If we reject the null hypothesis, this means that the null is:
a) False
b) True
c) Probably false
d) Unlikely to be true
e) None of the above
6) A result is statistically significant if:
a) The p-value is very low
b) The p-value is less than alpha
c) The p-value is greater than alpha
d) The mean of the sample is very different from the mean of the population
e) None of the above
7) If the null hypothesis is that the mean of the population from which we have sampled is 100 and the size of our sample is 36, what is the probability of observing a sample mean greater than 106 if the null is true:
a) .16
b) .14
c) .34
d) Unknown
8) If the null hypothesis is that the mean of the population from which we have sampled is 100, the size of our sample is 36, the SD of the population is 6 and the population is roughly Normal in shape, what is the probability of observing a sample mean greater than 106 if the null is true:
a) .16
b) .14
c) .34
d) Practically 0
e) Unknown
9) In question 8 above, the standard error of the mean is:
a) 6
b) 36
c) 1/6
d) 1
e) None of the above
10) The standard error of the mean is:
a) The standard deviation of the population
b) The standard deviation of the sampling distribution of the mean
c) The standard deviation of a sampling distribution
d) The standard deviation of the sample divided by the square root of the sample size
11) In hypothesis testing, we test:
a) The attendant assumptions
b) The null hypothesis
c) The alternative hypothesis
d) For statistical statistical significance
e) None of the above
12) If the observed value of Z is greater than the critical value of Z:
a) We reject the null hypothesis
b) We accept the null hypothesis
c) The p-value is lower than alpha
d) a and c
e) None of the above
13) In a two-tailed test:
a) There are two p-values
b) There are two alphas
c) There are two critical values
d) There is one rejection region
14) In a one-tailed test:
a) The p-value must less than 1/2 alpha in order to reject the null hypothesis
b) The p-value is smaller than in a two-tailed test
c) There is one rejection region
d) There are two rejection regions but they are smaller than in a one-tailed test
e) It is easier to reject the null hypothesis than in a two-tailed test
15) Suppose we had some reason to believe that our population bag may have been tampered with (some high or low chips might have been removed). We decide to make a decision about this by sampling 2 values from the bag. We decide that if the mean of the 2 values is 5 or 1, we will conclude that the bag has been tampered with (because sample means of 5 or 1 are unlikely if the bag has all the chips in it). What is our alpha in this case:
a) 1/25
b) 2/25
c) 1/5
d) Unknown